อสมการ - อ่านสารานุกรมไทย

          ประโยคที่มีตัวแปรและเชื่อมด้วยเครื่องหมายแสดงความไม่เท่ากัน เช่น 4x  20 นี้ เรียกว่า อสมการ การหาค่าของตัวแปรซึ่งจะทำให้ได้ข้อความจริง เรียกว่า  การแก้อสมการ

          การแก้อสมการที่เชื่อมด้วยเครื่องหมาย ทำได้ง่ายถ้าเราแก้สมการได้ เช่น ถ้าต้องการคำตอบของอสมการ 4x   20 เราก็หาคำตอบของสมการ  4x  = 20 เสียก่อน  ค่าของ x  ซึ่งไม่ได้คำตอบของสมการ  4x = 20 จะเป็นคำตอบของอสมการ 4x    20 ทั้งสิ้น

         สำหรับอสมการ 4x    20 นั้น ถ้ากำหนดว่า x จะต้องแทนจำนวนเต็มซึ่งไม่ใช่จำนวนลบ เราก็จะได้คำตอบ  6  คำตอบคือ 0,1,2,3,4,5 กรณีนี้คือ กรณีที่แม่ค้าขายส้มเต็มกิโลกรัมเท่านั้น ถ้าแม่ค้ายอมขายครึ่งกิโลกรัมด้วย คำตอบก็จะมี 0, 1, 1 1,  2,  2 1, 3, 3 1,  4,  4 1, 5 ถ้าแม่ค้าขายเป็นขีดด้วย คำตอบก็จะมีเพิ่มขึ้นอีก คือ 0,  .1,  .2,  .3,  .4,...,  4.6,  4.7,  4.8,  4.9,  5

          ถ้าต้องการแก้อสมการ 4x   20 เมื่อ x แทนจำนวนจริง เราจะได้คำตอบมากมาย กล่าวคือจำนวนจริงทุกจำนวนที่ไม่เกิน 5 เป็นคำตอบของอสมการนี้

          อสมการ 4x    20 เป็นตัวอย่างของอสมการเชิงเส้นที่มีตัวแปรเดียว อสมการแบบนี้เราแก้ได้โดยอาศัยหลักใหญ่ๆ ดังนี้คือ
          (1)  ถ้านำจำนวนๆ หนึ่ง มาบวกหรือลบทั้งสองข้างของเครื่องหมาย ซึ่งแสดงความไม่เท่ากัน อสมการใหม่จะมีคำตอบเหมือนอสมการเดิม
          (2)  ถ้านำจำนวนบวกมาคูณหรือหารทั้งสองข้างของเครื่องหมายซึ่งแสดงความไม่เท่ากัน อสมการใหม่จะมีคำตอบเหมือนอสมการเดิม
          (3)  ถ้านำจำนวนลบมาคูณทั้งสองข้างของเครื่องหมายซึ่งแสดงความมากกว่า อสมการใหม่ซึ่งมีคำตอบเหมือนอสมการเดิม จะต้องเชื่อมด้วยเครื่องหมายที่แสดงความน้อยกว่า
         (4)   ถ้านำจำนวนลบ มาคูณหรือหารทั้งสองข้างของเครื่องหมายซึ่งแสดงความน้อยกว่า อสมการใหม่ซึ่งมีคำตอบเหมือนอสมการเดิม จะต้องเชื่อมด้วยเครื่องหมายที่แสดงความมากกว่า

          อสมการต่อไปนี้มีคำตอบเหมือนกัน
                     2x + 3 > 5
                           2x > 2      นำ  3  มาลบทั้งสองข้าง
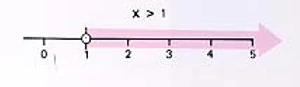
                             x > 1      นำ  2  มาหารทั้งสองข้าง
                              
         เราสรุปได้ว่าจำนวนใดๆ ซึ่งมากกว่า 1 เป็นคำตอบของอสมการ  2x + 3 > 5 อสมการต่อไปนี้มีคำตอบเหมือนกัน
                      3 - 2x    5
                          -2x   2         นำ  3   มาลบทั้งสองข้าง
                             x   -1         นำ -2  มาหารทั้งสองข้าง

         เราสรุปได้ว่า  -1  หรือจำนวนใดๆ ที่น้อยกว่า  -1 เป็นคำตอบของอสมการ  3 - 2x   5         อสมการอาจมีตัวแปรมากกว่า 1 ตัวแปรก็ได้ และวิธีแก้อสมการที่มีตัวแปรไม่เกิน  2  ตัวแปรเราสามารถใช้วิธีกราฟได้ ดังตัวอย่าง

         เราอาจจะใช้วิธีกราฟแก้ระบบอสมการได้ ดังต่อไปนี้
         กราฟแสดงคำตอบของระบบอสมการ
              2x + 3y       6
                  x - y       3

         ส่วนที่เป็นสีน้ำเงินคือคำตอบของอสมการ 2x + 3y   6 ส่วนที่เป็นสีแดง คือ คำตอบของอสมการ x - y   3 ส่วนตัดคือคำตอบของระบบอสมการที่ต้องการ