การวัดระยะทางบนพื้นราบ - อ่านสารานุกรมไทย

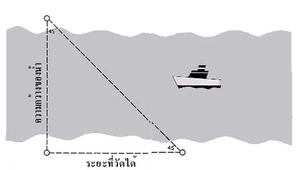
          เราทราบกันดีว่าระยะทางที่สั้นที่สุด ระหว่างจุดสองจุดบนพื้นราบคือความยาวของเส้นตรงที่ลากผ่านจุดทั้งสองนั้น ดังนั้นการหาระยะทางระหว่างจุดสองจุดนี้ เราอาจใช้เส้นเชือกหรือลวดขึงให้ตึงระหว่างสองจุดนั้น แล้วนำไปตรวจสอบความยาวกับไม้เมตรหรือไม้ฟุต ก็จะทราบความยาวที่ต้องการ ในทางช่างเขาใช้เส้นลวดที่แบ่งสเกลความยาวแล้ววัดระยะทางได้ทันที ถ้าระยะทางยาวกว่าเส้นลวดที่วัดก็จะต้องแบ่งความยาวออกเป็นช่วงๆ วัดความยาวแต่ละช่วงแล้วนำมารวมกัน
          ในการวัดระยะทางจริงๆ ระหว่างจุดสองจุดนี้ บางครั้งเราไม่อาจจะใช้เส้นลวดขึงให้ผ่านจุดทั้งสองได้ เช่น การวัดความกว้างของแม่น้ำ หรือมีสิ่งขวางกั้นระหว่างจุดทั้งสองนั้น กรณีเช่นนี้เราต้องวัดระยะโดยอ้อม และใช้หลักวิชาคณิตศาสตร์ช่วยคำนวณระยะทางที่ต้องการออกมาอีกครั้งหนึ่ง เช่น เราทราบว่าสามเหลี่ยมมุมฉากซึ่งมีมุมอีกสองมุมเท่ากัน คือ เท่ากับ 45 องศา ด้านประกอบมุมฉากของสามเหลี่ยมนั้นจะยาวเท่ากันพอดี เราเรียกสามเหลี่ยมชนิดนี้ว่า  สามเหลี่ยมมุมฉากหน้าจั่ว
          เราอาจใช้หลักวิชาเรขาคณิตในการคำนวณหาความสูง ชาวกรีกและชาวอียิปต์โบราณได้ใช้วิธีการนี้มานานหลายพันปีแล้ว หลักการของวิธีนี้ใช้คุณสมบัติของรูปสามเหลี่ยมที่มีมุมทั้งสามเท่ากันสองรูป ย่อมมีด้านทั้งสามเป็นสัดส่วนกันและกัน  เราเรียกสามเหลี่ยมทั้งสองว่าเป็นสามเหลี่ยมที่คล้ายกัน
          เมื่อวัดความสูงของต้นไม้ เช่น BC แทนความสูงของต้นไม้ วัดระยะจากโคนไม้คือ  B ไปยังจุด A จากจุด D ซึ่งอยู่ระหว่าง A และ B ใช้ไม้ที่ทราบขนาดความสูงแล้ววางให้ตั้งฉากกับพื้นดิน และเล็งจากจุด A ให้จุด A จุด  E และจุด C อยู่บนเส้นตรงเดียวกัน โดยใช้คุณสมบัติของสามเหลี่ยมคล้ายจะได้ BC/DE  =AB/ADหรือความสูง  BC  =  (AB.DE) /AD
เราอาจใช้เงาของวัตถุที่เกิดจากแสงอาทิตย์วัดความสูงก็ได้ เช่น ให้ AB เป็นความยาวของเงาต้นไม้ซึ่งเกิดจากดวงอาทิตย์ ตรงจุด A ซึ่งเป็นตำแหน่งปลายของเงาต้นไม้ เอาไม้ AD ซึ่งทราบขนาดความยาวแล้วมาปักตั้งฉากกับพื้นดิน เงาของ  AD จะทอดยาวออกไปถึงจุด E วัดระยะ AB และ  AE โดยอาศัยคุณสมบัติของรูปสามเหลี่ยมคล้ายจะได้  BC/AD=  BA/AEดังนั้น BC = AD.AB/AE
         วิธีการสร้างเครื่องมือวัดความสูงแบบง่ายๆ กระทำได้ดังนี้หากระดาษแข็งหรือไม้แผ่นบางๆขนาดกว้าง 10 นิ้ว ยาว 11 นิ้ว แบ่งสเกลทางด้านกว้างตั้งแต่ 0 ถึง 10 จะแบ่งสเกลของทุกหนึ่งนิ้วให้ละเอียดออกไปเป็น 10 ช่วงเล็กๆ เท่ากันทั้งหมดก็ได้ใช้ท่อนไม้ขนาดกว้าง 1 นิ้ว หนา 1 นิ้ว ยาว 10 นิ้ว ติดที่ขอบบนของกระดาษแข็งให้แน่น ส่วนของกระดาษแข็งที่อยู่ใต้ท่อนไม้จะเหลือกว้าง 10 นิ้ว ยาว 10  นิ้ว เอาด้ายถ่วงด้วยน้ำหนักพอสมควรมาผูกที่ปลายท่อนไม้ทางด้านขวามือ เมื่อวางท่อนไม้ขนานกับแนวระดับราบ เส้นด้ายจะอยู่ในตำแหน่งของเลข 0  ของสเกลข้างล่าง ติดห่วงเล็กๆ สองห่วงไว้บนท่อนไม้ให้ห่างจากกันประมาณ 9  นิ้ว ห่วงทั้งสองนี้ใช้สำหรับเล็งไปยังจุดที่ต้องการ เช่น ถ้าจะวัดความสูงของ  AB ก็ยกแผ่นไม้นี้เล็งไปยังจุด  A ซึ่งเป็นยอดสูงสุด อ่านตัวเลขที่เส้นดิ่งผ่านขอบล่างของแผ่นไม้ สมมุติว่าได้ n หน่วย วัดระยะจากจุดที่สังเกตไปยัง AB  สมมุติว่าได้  s  เมตร เอา n และ  s  คูณกันแล้วหารด้วย  10  แล้วบวกด้วยระยะที่จุดสังเกตอยู่สูงจากพื้นดิน   สมมุติว่าเท่ากับ a เมตร  ดังนั้นจะได้ความสูงของ  AB  คือ  h  จากสูตร
                           h  =  a + nxs
                                                      10
                ถ้า        a  = 1.6 เมตร  n = 3  หน่วย  s  =  30  เมตร
                จะได้ความสูง   h  = 1.6 + 3x30
                                                                     10
                                      = 10.6  เมตร

         เราอาจใช้สูตรในวิชาตรีโกณมิติหาระยะทางและความสูง โดยอาศัยด้านและมุมของรูปสามเหลี่ยม เช่น เราต้องการวัดระยะทางระหว่างจุดสองจุดบนฝั่งแม่น้ำฝั่งตรงกันข้าม  คือ  A  และ  B  เป็นจุดสองจุดบนฝั่งแม่น้ำฝั่งตรงกันข้ามที่เราต้องการวัดระยะทาง สมมุติว่าระยะทาง AB เท่ากับ x  เมตร  C และ D เป็นจุดซึ่งเราสามารถวัดระยะทางได้ s เมตร บนฝั่งซึ่งเรายืนอยู่  วัดมุม DCB  ได้มุม a วัดมุม  BCA  ได้มุม a'  วัดมุม  CDA  และ  ADB  ได้มุม  b และ  b' ตามลำดับ โดยใช้กฎเกณฑ์ในวิชาตรีโกณมิติเราสามารถแสดงได้ว่า

                             AC  = a sin b / sin (a+a'+ b)
             และ         BC  = a sin (b+b') / sin (a+b+b')
และหาความยาว  AB  ได้จากสูตร
                               x2 =  AC2 + BC2 - 2AB.BC cos a'

          จากตารางแสดงค่าฟังก์ชันตรีโกณมิติ เราก็สามารถคำนวณหาระยะทาง AB  ได้ทันที

           เราอาจจะประดิษฐ์เครื่องวัดมุมแบบง่ายๆ ได้ดังนี้ ใช้กระดาษแข็งหรือไม้อัดก็ได้มาตัดเป็นแผ่นวงกลมรัศมีประมาณ  3  นิ้ว เขียนวงกลมศูนย์กลางร่วมกันกับวงแรกใช้รัศมี 2 1/2 นิ้ว บนเส้นรอบวงกลมเล็กแบ่งออกเป็น 36  ส่วนเท่าๆ กัน แต่ละส่วนจะปิดมุมที่ศูนย์กลาง 10 องศาเท่ากัน ถ้าต้องการให้ละเอียดมากขึ้นก็ใช้ไม้บรรทัดที่มีการแบ่งมุมเป็นองศาซึ่งเรียกว่า ไม้โพรแทรกเตอร์ แบ่งสเกลบนวงกลมเล็กให้ครบ 360 องศาเลยก็ได้ ใช้เส้นลวดหรือเข็มเล็กๆ ที่สามารถเจาะรูที่ก้นได้สองอัน ใช้เข็มหมุดตรึงก้นเข็มทั้งสองไว้ตรงจุดศูนย์กลางวงกลม และให้เข็มทั้งสองสามารถหมุนไปได้รอบๆ แบบเข็มนาฬิกา เมื่อจะวัดมุมที่ใดก็เล็งจากหมุดตรงกลางให้เส้นลวดทั้งสองอยู่ในแนวที่ต้องการ ก็จะสามารถอ่านมุมระหว่างแนวทั้งสองได้ทันที