มีจุดคงที่หรือจุดโฟกัสสองจุดเช่นเดียวกับวงรี ถ้าเราให้จุดๆ หนึ่งเคลื่อนที่ไป โดยมีผลต่างของระยะทางระหว่างจุดที่เคลื่อนที่และจุดคงที่ทั้งสองมีค่าคงที่แล้ว จุดที่เคลื่อนที่ไปนั้นจะขีดรอยเส้นโค้งขึ้นซึ่งเรียกว่า เส้นโค้งไฮเพอร์โบลา และจะมีเส้นโค้งเช่นนี้ถึงสองส่วนโดยไม่ติดต่อกันเลย
ตามรูป F และ F' เป็นจุดคงที่สองจุด P เป็นจุดที่กำลังเคลื่อนที่โดยมีคุณสมบัติว่า PF'- PF = ค่าคงที่ = K ทางเดินของจุด P จะเป็นส่วนหนึ่งของเส้นโค้งไฮเพอร์โบลา แต่ถ้าเราให้ P' เป็นจุดที่กำลังเคลื่อนที่โดยมีคุณสมบัติว่า
P'F - P'F' = ค่าคงที่ = K
ทางเดินของจุด P ก็จะเป็นอีกส่วนหนึ่งของไฮเพอร์โบลาเดียวกัน
ถ้าลากเส้นตรงผ่าน F และ F' เส้นตรงนี้จะตัดส่วนทั้งสองของเส้นโค้ง ไฮเพอร์โบลาที่ A และ A' ซึ่งเราเรียกว่าจุดยอดของเส้นโค้ง เนื่องด้วย A และ A' ต่างก็อยู่บนเส้นโค้ง ดังนั้น AF'- AF = K = A'F - A'F'
จุด A และ A' ต่างก็เป็นจุดที่ และ AF = A'F' ดังนั้น K = AA' เท่ากับระยะห่างระหว่างจุดยอดทั้งสองของไฮเพอร์โบลา แสดงว่าผลต่างของระยะทางจากจุดโฟกัสไปยังจุดบนไฮเพอร์โบลานั้น เท่ากับระยะห่างระหว่างจุดยอดทั้งสองของไฮเพอร์โบลา
เราอาจจะเขียนเส้นโค้งไฮเพอร์โบลาด้วยไม้บรรทัด เส้นด้าย และดินสอ ดังนี้ กำหนดจุดคงที่ F และ F' ไว้บนกระดาษ ใช้เส้นด้ายที่มีความยาวน้อยกว่าความยาวของไม้บรรทัด และให้ผลต่างของความยาวของไม้บรรทัดและเส้นด้ายน้อยกว่าระยะทางระหว่าง F และ F' พอสมควร ใช้หมุดตรึงปลายข้างหนึ่งของไม้บรรทัดไว้ที่จุด F' ผูกปลายหนึ่งของเส้นด้ายไว้ที่จุด F และผูกอีกปลายหนึ่งไว้ที่ปลายอีกข้างหนึ่ง (ในรูปคือจุด B) ใช้ปลายดินสอดึงเส้นด้ายให้ตึงโดยให้เส้นด้ายส่วนหนึ่งอยู่ในแนวของไม้บรรทัดที่ค่อยๆ หมุนไป ปลายดินสอก็จะขีดรอยเส้นโค้งไฮเพอร์โบลาส่วนหนึ่งซึ่งอยู่เหนือเส้น FF' การเขียนส่วนโค้งส่วนที่อยู่ใต้ FF' ก็เพียงแต่วางไม้บรรทัดตามเส้นประ (ดังในรูป)
การเขียนส่วนที่สองของเส้นโค้ง ก็เปลี่ยนเอาปลายไม้บรรทัดอีกปลายหนึ่งให้หมุนรอบจุด F เอาเส้นด้ายผูกปลายไว้ที่ C และ F' และกระทำเช่นเดียวกันก็จะได้เส้นโค้งส่วนที่สอง
จากรูป PF' - PF = (PF'+ PB) - (PF + PB)
= CB - (PF + PB)
= ความยาวของไม้บรรทัด - ความยาวของด้าย
= ความยาวคงที่จำนวนหนึ่ง
= ระยะทางระหว่าง A และ A'
สมการทั่วไปของเส้นโค้งไฮเพอร์โบลามีแบบเป็น
x2/a2 - y2/b2 = 1
ถ้าสังเกตให้ดีจะเห็นว่ามีเส้นตรงสองเส้น ลากผ่านจุดกึ่งกลางของ FF' เส้นตรงสองเส้นนี้จะไปพบเส้นโค้งไฮเพอร์โบลาที่ระยะอนันต์ เส้นทั้งสองนี้มีลักษณะคล้ายเป็นกรอบของเส้นโค้ง
กราฟของสมการ xy = 1 ก็เป็นไฮเพอร์โบลาอีกแบบหนึ่งซึ่งมีแกน x และแกน y เป็นเส้นกรอบ และมีเส้นที่ทำมุม 45 องศากับแกน x เป็นแกนของรูป เส้นโค้งทั้งสี่ชนิดที่กล่าวมานี้คือ วงกลม วงรี พาราโบลาและไฮเพอร์โบลา เป็นเส้นโค้งที่ได้จากการตัดรูปกรวยมีฐานเป็นวงกลมด้วยพื้นราบ ในลักษณะต่างๆ กันดังนี้
ถ้าตัดด้วยพื้นราบซึ่งขนานกับฐาน จะได้รอยตัดเป็นวงกลม แต่ถ้าให้พื้นราบเอียงทำมุมพอสมควรกับฐานจะได้วงรี เมื่อพื้นราบเอียงจนขนานกับเส้นที่ลากจากจุดยอดของกรวยไปยังฐาน จะได้รอยตัดเป็นรูปพาราโบลา แต่ถ้าผ่ากรวยออกเป็นสองส่วนเท่าๆ กันโดยผ่านจุดยอดจะได้เส้นตรงคู่ ถ้าใช้กรวยขนาดเท่ากันสองกรวยวางให้จุดยอดต่อกัน (ดังรูป) แล้วตัดด้วยพื้นราบซึ่งตั้งได้ฉากกับฐานของกรวย จะได้รอยตัดเป็นรูปไฮเพอร์โบลาสองส่วนอยู่บนกรวยแต่ละส่วน เราจึงถือว่า วงกลม วงรี พาราโบลา ไฮเพอร์โบลา และเส้นตรงคู่เป็นเส้นโค้งจากภาคตัดของกรวย (conic sections)
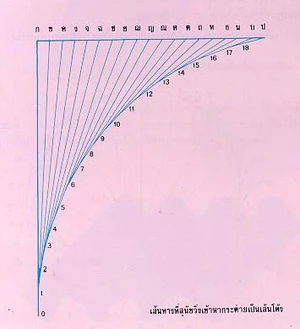
เขียนวงกลมรัศมี 2 1/4 นิ้ว จากจุดศูนย์กลางเขียนเส้นรังสี 18 เส้นให้ทำมุมเท่ากับ 20 องศาเท่าๆ กันโดยใช้ไม้โพรแทรกเตอร์ (ไม้ที่มีสเกลแบ่งมุม) ให้ตัวเลขรังสีเริ่มจาก 0 ถึง 17 แล้วต่อไปเป็น 18, 19, 20,...ตามรูป กำหนดจุดบนเส้นรังสีเหล่านี้ จุดแรกบนรังสีที่หนึ่งอยู่ห่างจากจุดศูนย์กลาง 1/8นิ้ว จุดที่สองบนรังสีที่สองอยู่ห่างจากจุดศูนย์กลาง 2/8นิ้ว จุดที่สามบนรังสีที่สามอยู่ห่างจากจุดศูนย์กลาง 3/8นิ้ว ทำเช่นนี้ไปจนถึงรังสีที่ 18 จุดจะอยู่บนวงกลมพอดี ถ้าทำต่อไปโดยให้ความยาวของรังสีเพิ่มขึ้นครั้งละ 1/8 นิ้ว แล้วโยงจุดเหล่านี้เข้าด้วยกัน จะได้เส้นโค้งเป็นรูปก้นหอย (spiral)
จากวิธีการเขียนเส้นโค้งก้นหอย จะเห็นได้ว่าถ้าให้ O เป็นจุดคงที่ เส้น OX เป็นเส้นที่อยู่คงที่เส้นหนึ่ง เส้นตรงใดๆ ที่ลากผ่าน O มีความยาว r และทำมุม q กับเส้น OX เราเรียกเส้น OP ว่ารังสี OP การวัดมุม q วัดจาก OX ไป หา OP ในทิศทางทวนเข็มนาฬิกาถือว่าเป็นการวัดไปในทิศทางบวก มุม q จะวัดในหน่วยองศาหรือเรเดียนก็ได้ (มุม 1เรเดียน คือมุมที่ศูนย์กลางของวงกลมซึ่งรองรับส่วนโค้งของเส้นรอบวงของวงกลม มีความยาวเท่ากับรัศมีของวงกลมนั้น มุม 2p เรเดียน เท่ากับ 360 องศา และมุม 1 เรเดียนเท่ากับ 57.28 องศาโดยประมาณ) การวัดมุมอาจจะวัดกี่รอบก็ได้ เราบอกตำแหน่งของจุด P ด้วยขนาดของความยาว r ของรังสี OP และขนาดของมุม q ที่ OP ทำกับเส้น OX และเขียนแสดงโดยคู่ลำดับ (r,q)
จุดต่างๆ บนเส้นโค้งก้นหอยสร้างจากหลักเกณฑ์ "ความยาวของรังสี OP เป็นปฏิภาคโดยตรงกับขนาดของมุมที่ OP ทำกับเส้น OX" เขียนเป็นสมการดังนี้
r = aq
เมื่อ a เป็นค่าคงที่ เราเรียกเส้นโค้งแบบนี้ว่า เส้นโค้งก้นหอยแบบอาร์คีมีดีส (Spiral of Archimedes) ถ้าลองกลับไปดูความยาวของเส้นรังสี ที่วัดจากจุดศูนย์กลางไปยังจุดบนเส้นโค้งก้นหอยแบบอาร์คีมีดีส จะเห็นว่าความยาวจะเพิ่มขึ้นเป็นความก้าวหน้าเลขคณิต ดังนี้
1/8,2/8,3/8,4/8, 5/8,6/8, 7/8, ...
เราอาจจะสร้างเส้นโค้งก้นหอยอีกแบบหนึ่ง ให้ความยาวของรังสีค่อยๆ เพิ่มขึ้นแบบความก้าวหน้าเรขาคณิตก็ได้ เมื่อมุมของรังสีเท่ากันหมดที่จุดศูนย์กลาง เส้นโค้งก้นหอยที่น่าสนใจแบบหนึ่งมีความยาวของรังสีที่อยู่ห่างกัน 12 พจน์ เป็น 2 เท่ากัน กล่าวคือ ถ้าความยาวของรังสีเรียงตามลำดับแบบความก้าวหน้าเรขาคณิต
r, r2, r3,...rn,...
เมื่อแทนรังสีที่ n ด้วย rn ดังนั้น rn = rn จะได้
rn + 12 = 2rn หรือ rn+12 = 2rn
ดังนั้น r12 = 2 หรือ r = 1.0595
แบ่งมุมรอบจุด O ออกเป็น 24 ส่วนเท่าๆ กันโดยเส้นรังสี Oa, Ob, Oc, B, C,...บนเส้นรังสี Oa, Ob, Oc,...ดังต่อไปนี้
จุด A อยู่บน Oa ให้ OA = 1.00 หน่วย
จุด B อยู่บน Ob ให้ OB = 1.06 หน่วย
จุด C อยู่บน Oc ให้ OC = 1.12 หน่วย
จุด D อยู่บน Od ให้ OD = 1.19 หน่วย
จุด E อยู่บน Oe ให้ OE = 1.26 หน่วย
จุด F อยู่บน Of ให้ OF = 1.33 หน่วย
จุด G อยู่บน Og ให้ OG = 1.41 หน่วย
จุด H อยู่บน Oh ให้ OH = 1.50 หน่วย
จุด I อยู่บน Oi ให้ OI = 1.59 หน่วย
จุด J อยู่บน Oj ให้ OJ = 1.68 หน่วย
จุด K อยู่บน Ok ให้ OK = 1.78 หน่วย
จุด L อยู่บน Ol ให้ OL = 1.89 หน่วย
จุด M อยู่บน Om ให้ OM = 2.00 หน่วย
จุด N อยู่บน On ให้ On = 2.12 หน่วย
จุด P อยู่บน Op ให้ Op = 2.24 หน่วย
จุด Q อยู่บน Oq ให้ Oq = 2.38 หน่วย
จุด R อยู่บน Or ให้ OR = 2.52 หน่วย
จุด S อยู่บน Os ให้ OS = 2.66 หน่วย
จุด T อยู่บน Ot ให้ OT = 2.83 หน่วย
จุด U อยู่บน Ou ให้ OU = 3.00 หน่วย
จุด V อยู่บน Ov ให้ OV = 3.17 หน่วย
จุด W อยู่บน Ow ให้ Ow = 3.36 หน่วย
จุด X อยู่บน Ox ให้ OX = 3.56 หน่วย
จุด Y อยู่บน Oy ให้ Oy = 3.77 หน่วย
จุด A' อยู่บน Oa ให้ OA' = 4.00 หน่วย
จุด B' อยู่บน Ob ให้ OB' = 4.24 หน่วย
จุด C' อยู่บน Oc ให้ OC' = 4.49 หน่วย
จากการสังเกตจะเห็นว่า
OA' = 4 OA
OB' = 4 OB
OC' = 4 OC
...................
OA" = 4 OA' = 16 OA
OB" = 4 OB' = 16 OB
OC" = 4 OC' = 16 OC
