สมการบางสมการอาจจะไม่มีคำตอบ เช่น ถ้าถามว่า "มีจำนวนเต็มจำนวนใดบ้างซึ่งคูณกับ 2 แล้วได้ 3" ก็ต้องตอบว่า "ไม่มีจำนวนเต็มเช่นนั้น" เราพูดได้อีกอย่างหนึ่งว่า สมการ 2x = 3 ไม่มีคำตอบซึ่งเป็นจำนวนเต็ม
เราทราบว่าจำนวนจริงใดๆ ก็ตามเมื่อคูณกับตัวเองแล้วย่อมไม่ได้จำนวนลบ ดังนั้น เราพูดว่า สมการ X x X = -1ซึ่งเขียนได้ว่า x2 = -1 ไม่มีคำตอบเป็นจำนวนจริง
สมการบางสมการอาจมีคำตอบมากกว่าหนึ่งคำตอบ เช่น ถ้าถามว่า "จำนวนใดคูณกับตัวเองแล้วได้ 1" ก็ต้องตอบว่า "-1 และ 1" หรือพูดว่าสมการ x2 = 1 มีคำตอบ 2 คำตอบ คือ -1 และ 1
สมการที่มีตัวแปรเดียวและเลขชี้กำลัง* ของตัวแปรเป็น 1 เราเรียกว่าสมการเชิงเส้น (Linear equation) ที่มีตัวแปรเดียว ดังนั้น 2x - 5 = 1, 6 + 3x = 2, 3t + 1 - 2y = 2.7, 2z - 10 = 0 ล้วนเป็นตัวอย่างของสมการเชิงเส้นที่มีตัวแปรเดียว
การแก้สมการเชิงเส้นที่มีตัวแปรตัวเดียว เรามีหลักการใหญ่ๆ ดังนี้ คือ
(1) ถ้านำจำนวนๆ หนึ่งมาบวก หรือลบทั้งสองข้างของเครื่องหมาย = เราจะได้สมการ ซึ่งมีคำตอบเหมือนสมการเดิม
(2) ถ้านำจำนวนๆ หนึ่ง ซึ่งไม่ใช่ 0 มาคูณ หรือหารทั้งสองข้างของเครื่องหมาย = เราจะได้สมการซึ่งมีคำตอบเหมือนสมการเดิม
สมมุติว่าเราต้องการแก้สมการ 2x + 3 = 5 เราใช้หลักทั้งสองข้อดังนี้
2x + 3 = 5
2x = 2 นำ 3 มาลบทั้งสองข้าง
x = 1 นำ 2 มาหารทั้งสองข้าง
จากหลักทั้งสองข้อ เราได้ว่าสมการทั้งสามนี้มีคำตอบเหมือนกัน ดังนั้นเราจึงสรุปได้ว่า 1 เป็นคำตอบของสมการ 2x + 3 = 5
* เราเขียน 5 ได้ว่า 51 และเรียก 1 ว่า เลขชี้กำลัง
เราเขียน 5 x 5 ได้ว่า 52 และเรียกเลข 2 ว่า เลขชี้กำลัง
เราเขียน 5 x 5 x 5 ได้ว่า 53 และเรียกเลข 3 ว่า เลขชี้กำลัง ฯลฯ
ให้ x แทนจำนวนใด ๆ ก็ตาม
เราเขียน X ได้ว่า X1 และเรียกเลข 1 ว่า เลขชี้กำลัง
เราเขียน X x X ได้ว่า X2 และเรียกเลข 2 ว่า เลขชี้กำลัง
เราเขียน X x X x X ได้ว่า X3 และเรียกเลข 3 ว่า เลขชี้กำลัง
เราเขียน X x X x X x X x X ได้ว่า X5 และเรียกเลข 5 ว่า เลขชี้กำลัง ฯลฯ
เลขชี้กำลังไม่จำเป็นต้องเป็นจำนวนเต็มบวก แต่เราจะไม่กล่าวถึงในที่นี้
หลักข้อ (2) ห้ามนำ O มาหารทั้งสองข้างของเครื่องหมาย = ในสมการ เพราะการหารด้วย O ไม่มีความหมาย และหลักเดียวกันนี้ห้ามนำ O มาคูณทั้งสองข้างของเครื่องหมาย = ในสมการ เพราะสมการใหม่จะมีคำตอบต่างจากสมการเดิม ตัวอย่างเช่น สมการ 2x = 6 มีคำตอบเพียงคำตอบเดียว ได้แก่ 3 แต่สมการ 2X x 0 = 6x0 นั้นมีจำนวนจริงทุกจำนวนเป็นคำตอบ เนื่องจากจำนวนจริงใดๆ ก็ตามคูณกับ O แล้วย่อมได้ O
ควรสังเกตว่า การพูดกว้างๆ ว่า "ในการแก้สมการนั้น ถ้าทำอย่างไรทางซ้าย (ของเครื่องหมาย =) แล้วให้ทำอย่างเดียวกันทางขวา (ของเครื่องหมาย =)" นั้น ใช้ไม่ได้ เพราะสมการใหม่อาจมีคำตอบต่างจากสมการเดิมได้ เช่น สมการ x = 3 กับสมการ x2 = 32 ซึ่งได้จากการ "ยกกำลังสองทั้งสองข้าง" มีคำตอบต่างกัน สมการ x = 3 มีคำตอบเพียงคำตอบเดียวคือ 3 ส่วนสมการ x2 = 32 มีคำตอบ 2 คำตอบ คือ -3 กับ 3
สมการ x-1 = 0 กับสมการ x (x-1) = 0 ก็มีคำตอบต่างกัน สมการที่สองได้จากการคูณ x ทั้งสองข้าง (ของเครื่องหมาย =) ในสมการแรก หรือจะพูดว่าสมการแรกได้จากการหารด้วย x ทั้งสองข้างในสมการที่สองก็ได้ สมการ x-1 = 0 มีคำตอบเพียงคำตอบเดียวคือ 1ส่วนสมการ x (x-1) = 0 มีคำตอบ 2 คำตอบ คือ 0 และ 1
สมการอาจจะมีตัวแปรกี่ตัวแปรก็ได้ เช่น โจทย์ที่ว่า "จงหาจำนวนสองจำนวนซึ่งมีผลต่างเป็น 3" อาจจะเขียนได้ว่า "จงแก้สมการ x-y = 3" สมการ x-y = 3 เป็นสมการที่มีตัวแปร 2 ตัว สมการนี้มีคำตอบมากมาย เช่น x = 4 และ y = 1 หรือ x = 3 และ y = 0 หรือ x = และ y = -3 เป็นต้น คำตอบเหล่านี้เรานิยมเขียนในรูปคู่ลำดับว่า (4,1), (3,0) , ( ) จำนวนแรกในคู่ลำดับแทนค่า x จำนวนหลังแทนค่า y ดังนั้น (4,1) เป็นคำตอบหนึ่งๆ ของสมการ x - y = 3 แต่ (1,4) ไม่ใช่คำตอบของสมการนี้
เนื่องจากสมการ x - y = 3 นี้ มีคำตอบที่เป็นจำนวนจริงอยู่มากมาย ไม่สามารถแจกแจงให้ดูได้หมด วิธีที่จะแสดงคำตอบได้วิธีหนึ่งคือ การเขียนกราฟ
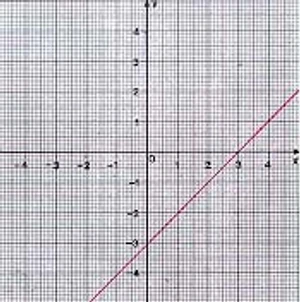
สมการที่มีตัวแปรเดียวก็สามารถแก้ได้โดยวิธีกราฟ เช่น ถ้าต้องการแก้สมการ 2x + 3 = 5 ซึ่งมีคำตอบเหมือนสมการ 2x - 2 = 0 (นำ 5 มาลบทั้งสองข้างของเครื่องหมาย =) เราเพิ่มตัวแปร y ขึ้นมาอีกหนึ่งตัว โดยกำหนดให้ 2x -2 = y
สมการนี้เป็นสมการที่มีตัวแปรสองตัว คำตอบของสมการ 2x - 2 = y คือทุกจุดที่อยู่บนเส้นตรงสีแดง ค่าของ x ที่ทำให้ y เป็น 0 เป็นคำตอบของสมการ 2x-2 =0 จุดบนกราฟที่ y เป็น 0 คือจุดที่กราฟตัดแกนนอน เส้นตรงนี้ตัดแกนนอนที่จุด (1,0)
เราจึงสรุปได้ว่า 1 เป็นคำตอบของสมการ 2x - 2 = 0
หรือสมการ 2x + 3 = 5
สมการ x2 - 2x = 3 มีคำตอบเหมือนสมการ x2 - 2x - 3 = 0 เราแก้ได้โดยเขียนกราฟแสดงคำตอบของสมการ x2 - 2x - 3 = y (เส้นโค้งสีน้ำเงินในรูป) ค่าของ x ที่ทำให้ y เป็น 0 เป็นคำตอบของสมการ x2 - 2x - 3 = 0 จุดบนกราฟที่ y เป็น 0 คือจุดที่กราฟตัดแกนนอนได้แก่จุด (-1,0) และ (3,0)
เราจึงสรุปว่า -1 กับ 3 เป็นคำตอบของสมการ x2 - 2x - 3 = 0 หรือ x2 - 2x = 3
ในการแก้สมการ x2 - 2x + 2 = 0 เราเขียนกราฟแสดงคำตอบของสมการ x2 - 2x + 2 = y จะพบว่ากราฟนั้นไม่ตัดแกนนอน แสดงว่าจุด (x,0) ไม่อยู่บนกราฟ ดังนั้น (x,0) ไม่ใช่คำตอบของสมการ x2 - 2x + 2 = y นั่นคือไม่ว่า x จะแทนจำนวนจริงใดๆ ก็ตาม x2 - 2x + 2 ไม่เท่ากับ 0 เราจึงสรุปได้ว่าสมการ x2 -2x + 2 = 0 ไม่มีคำตอบที่เป็นจำนวนจริง
ตัวอย่างของโจทย์ปัญหาประเภทนี้คือ "มีส้มอยู่จำนวนหนึ่ง ถ้าจะแบ่งให้คน 5 คนๆ ละเท่าๆ กัน จะขาดส้ม 1 ผล ถ้าจะแบ่งให้คน 7 คนๆ ละเท่าๆ กัน ก็จะขาด 1 ผล ถามว่ามีส้มอยู่เท่าไร"
ถ้าสมมุติว่ามีส้มอยู่ n ผล เราจะได้ว่า n+1 หารด้วย 5 ลงตัว และหารด้วย 7 ก็ลงตัว นั่นคือ n+1 = 5x และ n+1 = 7y เมื่อ x และ y แทนจำนวนเต็มบวก
เราจึงต้องแก้สมการ 5x = 7y เมื่อ x และ y แทนจำนวนเต็มบวก
จะเห็นว่าสมการนี้มีคำตอบมากมายได้แก่ (7,5), (14,10), (21,15), (28,20), (35,25), (42,30),... คำตอบเหล่านี้ให้ค่า 5x (หรือ 7y) เป็น 35, 70, 105, 140, 175, 210,... ตามลำดับ ดังนั้นค่าของ n ที่ต้องการคือ 34, 69, 104, 139, 174, 209,... ถ้าโจทย์ถามเพิ่มเติมว่าจำนวนส้มน้อยที่สุดเป็นเท่าไร จึงจะมีลักษณะตามที่ต้องการ ก็จะได้คำตอบ 34
สมการไดโอแฟนทีนมีอยู่มากมายหลายประเภท สมการไดโอแฟนทีนที่มีชื่อเสียงมากสมการหนึ่งคือ สมการ x2 + y2 = z2 ซึ่งเราเรียกกันว่า สมการปีทาโกเรียน (Pythagorean equation) ชื่อนี้ตั้งขึ้นเพื่อเป็นเกียรติแก่ ปีทาโกรัส*(Pythagorus) การหาคำตอบที่เป็นจำนวนบวกของสมการนี้ก็คือ การหาความยาวที่เป็นจำนวนเต็มของด้านทั้งสามของสามเหลี่ยมมุมฉากนั่นเอง คำตอบที่เราทราบกันดีคือ x=3, y=4, z=5 ซึ่งเขียนได้อีกอย่างหนึ่งว่า (3,4,5) สมการปีทาโกเรียนนี้มีคำตอบมากมายนับได้ไม่หมด คำตอบทั้งหลายหาได้จากสูตรต่อไปนี้ คือ
x = a2 - b2,y = 2ab และ z = a2 + b2 เมื่อ a และ b แทนจำนวนเต็ม เช่น ถ้าให้ a = 2 และ b = 1 เราจะได้คำตอบ (3,4,5) ถ้าให้ a = 3 และ b = 2 เราจะได้คำตอบ (5,12,13) ถ้าให้ a = 3 และ b = 1เราจะได้คำตอบ (8,6,10) เป็นต้น
เรากล่าวได้ว่าสมการปีทาโกเรียนนั้น เราทราบคำตอบได้อย่างสมบูรณ์เพราะเรามีวิธีหาคำตอบทั้งหมดได้
สมการไดโอแฟนทีนที่มีตัวแปร 2 ตัว และเป็นการเชิงเส้น เช่น 5x = 7y, 6x + 15y = 12 ฯลฯ เราทราบคำตอบได้อย่างสมบูรณ์ แต่สมการไดโอแฟนทีนส่วนใหญ่ยังไม่ทราบคำตอบอย่างสมบูรณ์ บางสมการยังไม่ทราบเลยด้วยซ้ำไปว่ามีคำตอบหรือไม่ เช่น สมการ xn + yn = zn เมื่อ n เป็นจำนวนเต็มซึ่งมากกว่า 2 สมการนี้ไม่มีใครทราบเลยว่ามีคำตอบเป็นจำนวนเต็มบวกหรือไม่
แฟร์มาต์* ทำนายไว้ว่า "สมการ xn + yn = zn ไม่มีคำตอบเป็นจำนวนเต็มบวก เมื่อ n เป็นจำนวนเต็มที่มากกว่า 2" ข้อความนี้เขียนได้อีกอย่างหนึ่งว่า "ไม่ว่า x, y, z, n จะเป็นจำนวนเต็มบวกใดๆ ก็ตาม ถ้า n มากกว่า 2 แล้ว จะได้ว่า xn + yn zn" ข้อความนี้เรียกกันว่า ทฤษฏีบทสุดท้ายของแฟร์มาต์ (Fermat's Last Theorem) ในระยะเวลา 300 กว่าปีที่ผ่านมานี้ นักคณิตศาสตร์หลายคนพยายามพิสูจน์ข้อความนี้ และมีผู้ค้นพบข้อความนี้เป็นข้อความจริงสำหรับหลายค่าของ n เช่น มีผู้พิสูจน์ได้ว่า "ไม่ว่า x,y,z,n จะเป็นจำนวนเต็มบวกใดๆ ก็ตาม ถ้า n มากกว่า 2 และน้อยกว่า 100 แล้ว จะได้ว่า xn + yn zn" แต่จนบัดนี้ก็ยังไม่มีใครสามารถพิสูจน์ได้ว่า ทฤษฎีบทสุดท้ายของแฟร์มาต์ เป็นข้อความจริงหรือเท็จ
ความจริง ปัญหาคณิตศาสตร์ที่เกิดในชีวิตประจำวันมักจะไม่ใช่ปัญหาสมการ เช่น ถ้าเราต้องการซื้อของ เราก็มักจะใช้ซื้อจนเงินหมดกระเป๋า เพียงแต่ซื้อไม่ให้เกินเงินที่มีอยู่เท่านั้น เช่น มีเงิน 20 บาท จะซื้อส้มเขียนหวานราคากิโลกรัมละ 4 บาท เราอาจจะไม่ซื้อจนหมดเงิน เราอาจจะซื้อเพียง 1 กิโลกรัม หรือ 2 กิโลกรัมเท่านั้น แต่เราจะซื้อเกิน 5 กิโลกรัมไม่ได้ ถ้าสมมุติว่าซื้อ x กิโลกรัม จะสิ้นเงิน 4x บาท ถ้าซื้อจนหมดเงิน จะเขียนได้เป็นสมการ 4x = 20 แต่โดยปกติแล้วเราไม่จำเป็นต้องซื้อจนหมดเงิน เราจึงกำหนดเพียงว่า 4x ต้องไม่มากกว่า 20 หรือ 4x น้อยกว่าหรือเท่ากับ 20 ซึ่งเขียนได้อีกอย่างหนึ่งว่า 4x 20
เครื่องหมายที่แสดงความไม่เท่ากันที่นิยมใช้กันมีดังต่อไปนี้
> แทนคำว่า มากกว่า
" มากกว่าหรือเท่ากับ
< " น้อยกว่า
" น้อยกว่าหรือเท่ากับ
" ไม่เท่ากับ
* ไดโอแฟนทัสมีชีวิตอยู่ในสมัยประมาณ 250 ปี ก่อนคริสต์ศักราช เป็นชาวเมืองอเล็กซานเดรีย เราไม่ค่อยทราบรายละเอียดเกี่ยวกับชีวิตของเขามากนัก แต่อาจจะคำนวณอายุของเขาได้จากคำซึ่งเล่ากันต่อๆ มาดังนี้
เขาเป็นเด็กอยู่ 1 ของอายุของเขา เป็นวัยรุ่นอยู่ 1 ของอายุ เป็นชายโสดอยู่ 1 ของอายุ ลูกชายของเขาเกิดเมื่อเขาแต่งงานแล้ว 5 ปี ลูกชายตายก่อนเขา 4 ปี เขามีอายุยืนเป็น 2 เท่าของลูกชาย (คำตอบคือ 84 ปี)
* ปีทาโกรัส เป็นนักปรัชญาและนักคณิตศาสตร์ชาวกรีกมีชีวิตอยู่ระหว่างปี 582-507 ปีก่อนคริสต์ศักราช ทฤษฎีบทของเขาซึ่งเรารู้จักกันดี คือทฤษฎีบทในเรขาคณิตที่กล่าวว่ากำลังสองของความยาวด้านตรงข้ามมุมฉากของสามเหลี่ยมมุมฉากใดๆ ย่อมเท่ากับผลบวกของกำลังสองของความยาวอีกสองด้าน
*แฟร์มาต์ (ค.ศ. 1601-1665) เป็นชาวฝรั่งเศส อาชีพรับราชการ งานอดิเรกคือ คณิตศาสตร์ ถือได้ว่าเป็นคนหนึ่งที่ริเริ่มเรขาคณิตวิเคราะห์และแคลคูลัสแต่ปัจจุบันคนรู้จักเขามากจากผลงานของเขาเรื่องทฤษฎีของจำนวน (Theory of Numbers)
