เมื่อเราขว้างวัตถุขึ้นไปในอากาศ จะสังเกตได้ว่าเส้นทางของวัตถุที่เคลื่อนไปนั้นจะเป็นเส้นโค้ง ทั้งนี้เพราะวัตถุนั้นถูกโลกดึงดูดลงมา วิถีของลูกกระสุนปืนใหญ่ที่ยิงออกไปก็จะเดินทางเป็นเส้นโค้งชนิดเดียวกันกับตัวอย่างข้างบน เราเรียกเส้นโค้งชนิดนี้ว่า พาราโบลา
ลองพิจารณาตัวเลขต่อไปนี้ 0, 1, 4, 9, 16, 25, 36, 49,... ซึ่งได้จากการเอาเลขจำนวนเต็มคูณตัวเองคือ 0 x 0, 1 x 1, 2 x 2, 3 x 3, 4 x 4, 5 x 5, 6 x 6, 7 x 7,... ถ้าแทนเลขจำนวนเต็มด้วย x และแทนจำนวนยกกำลังสองด้วย y จะได้
x = 0 1 2 3 4 5 6 7 8...
y = 0 1 4 9 16 25 36 49 64...
ความสัมพันธ์ของจำนวนสองชุดนี้ จะเขียนเป็นสมการได้ดังนี้
เมื่อลงจุด (x, y) บนกระดาษกราฟ แล้วโยงจุดต่างๆ ด้วยเส้นโค้งจะได้ส่วนหนึ่งของพาราโบลา
เนื่องจาก (-2) x (-2) = 4 ดังนั้นสำหรับค่า y หนึ่งค่าจะเกิดจากค่า x สองค่า คือ ค่า x ที่เป็นบวกค่าหนึ่ง และค่าของx ที่เป็นลบค่าหนึ่ง ซึ่งเมื่อต่างยกกำลังสองกำลังจะได้ค่า y เท่ากัน คือ y = x2
เมื่อนำไปเขียนตารางค่า x และ y จะได้ x -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 y 64 49 36 25 16 9 4 1 0 1 4 9 16 25 36 49 64
เมื่อลงจุดเหล่านี้บนกระดาษกราฟ จะได้พาราโบลา ถ้าพับรูปตามแกน y เส้นโค้งทั้งสองข้างของแกน y จะทับกันสนิท เราเรียกแกน y ว่า เป็นแกนของเส้นโค้ง และเส้นโค้งมีสมมาตรเมื่อเทียบกับแกน y
จากหลักวิชาของแสง เราทราบว่า เมื่อแสงเดินทางมากระทบวัตถุสะท้อนแสง เช่น กระจกเงา มุมที่อยู่ระหว่างลำแสงตกและกระจกเงาจะเท่ากับมุมที่อยู่ระหว่างลำแสงสะท้อนและกระจกเงา เรียกสั้นๆ ว่า มุมตกเท่ากับมุมสะท้อน ในกรณีที่วัตถุสะท้อนแสงเป็นผิวโค้ง(เรายังคงใช้กฎการสะท้อนแสงได้เช่นเดียวกัน) โดยลากเส้นตรงเส้นหนึ่งสัมผัสกับเส้นโค้งตรงจุดที่ลำแสงกระทบกับผิวโค้งนั้น
จากการทดลองพบว่า ถ้าวัตถุสะท้อนแสงเป็นผิวโค้งซึ่งมีรอยตัดเป็นพาราโบลา แล้วให้ลำแสงขนานกับแกนของเส้นโค้งมากระทบพาราโบลานี้ ลำแสงที่สะท้อนออกจากเส้นโค้งนี้จะไปพบกันที่จุดเดียวกันบนแกนของเส้นโค้งนี้เสมอเราเรียกจุดนี้ว่า จุดโฟกัส ของเส้นโค้งพาราโบลา หรือถ้าเราเอาดวงไฟไปวางไว้ตรงจุดโฟกัสนี้ ลำแสงที่สะท้อนออกจากพาราโบลาก็จะพุ่งออกไปขนานกันกับแกนของรูปเสมอ โดยอาศัยคุณสมบัติพิเศษนี้เราจะเห็นได้ว่าโคมไฟฉาย โคมไฟรถยนต์ส่วนมากจะมีลักษณะเป็นผิวโค้ง ที่เกิดจากการหมุนพาราโบลารอบแกน (ดูหัวข้อผิวโค้งที่เกิดจากการหมุนเส้นโค้ง)
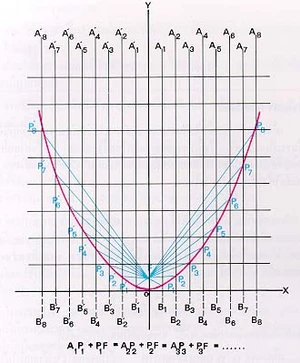
เนื่องจากแสงเดินทางได้ระยะทางเท่ากันในเวลาเท่ากัน ฉะนั้นแสงที่เดินทางจากจุด A1, A2, A3,... ไปกระทบเส้นโค้งพาราโบลาที่จุด P1, P2, P3,... แล้วสะท้อนออกไปพบกันที่จุด F พร้อมกัน ดังนั้น
A1P1 + P1F = A2P2 + P2F = A3P3 + P3F = ...
ถ้าต่อ A1P1, A2P2, A3P3,... ออกไปจนถึงจุด B1, B2 B3,... โดยทำให้ P1B1 = P1F, P2B2 = P2F, P3B3 = P3F,...เราจะพบว่าจุด B1, B2, B3, ... อยู่บนเส้นตรงเดียวกัน ซึ่งขนานกับแกน x และอยู่ใต้แกน x เท่ากับระยะที่จุด F อยู่เหนือแกน x นั่นคือพาราโบลาเกิดจากจุดซึ่งเคลื่อนที่ไปโดยมีระยะ ทางห่างจากจุดคงที่ (คือจุดโฟกัส) เท่ากับระยะทางจุดนั้นห่างจากเส้นตรงคงที่เส้นหนึ่ง เราเรียกเส้นตรงคงที่นี้ว่า ไดเรกตริกซ์ (directrix) ของรูป และเรียกเส้นตรงซึ่งตั้งได้ฉากกับไดเรกตริกซ์และผ่านจุดโฟกัสว่าแกนของพาราโบลา
โดยอาศัยคุณสมบัตินี้เราอาจนำมาประดิษฐ์เครื่องมือเขียนเส้นโค้งพาราโบลาได้ดังนี้ กำหนดเส้นตรงคงที่เส้นหนึ่งและจุดคงที่จุดหนึ่งบนกระดาษ โดยให้จุดคงที่นี้อยู่นอกเส้นตรงคงที่ ใช้ไม้บรรทัดอันหนึ่งวางทาบตามแนวเส้นตรงคงที่ และไม้ฉากรูปสามเหลี่ยมอีกอันหนึ่งวางทาบกับไม้บรรทัดอันแรกตามรูป ใช้เส้นด้ายที่มีความยาวเท่ากับความยาวของไม้ฉากด้าน AB ผูกปลายหนึ่งของด้ายไว้ที่จุด A บนปลายของไม้ฉาก และผูกอีกปลายหนึ่งของด้ายไว้ที่จุดคงที่ F (เมื่อผูกปลายด้านทั้งสองแล้วให้เส้นด้ายมีความยาวเท่ากับด้าน AB พอดี) ใช้ปลายดินสอวางที่เส้นด้ายตรงจุด P บนด้าน AB โดยให้เส้นด้ายตึงอยู่ตลอดเวลาค่อยๆ เลื่อนไม้ฉากไปตามบรรทัด ปลายดินสอจะขีดเส้นโค้งพาราโบลาส่วนหนึ่งที่อยู่เหนือแกนของรูป ซึ่งเป็นเส้นตรงที่ผ่านจุดคงที่และตั้งฉากกับเส้นตรงคงที่ การเขียนเส้นโค้งอีกส่วนหนึ่งก็กระทำคล้ายๆ กัน โดยวางไม้ฉากตามแนวประในภาพ เราจะเห็นได้ว่า
PA + PF = PA + PB = AB
ดังนั้น PF = PB
เส้นโค้งที่จะได้เป็นเส้นโค้งพาราโบลา
จากการทดลองปล่อยวัตถุให้ตกลงมาจากที่สูง วัตถุจะถูกแรงดึงดูดของโลกดูดลงมาจนกระทบพื้นดิน ถ้า y เป็นระยะทางที่วัตถุตกลงมา (โดยวัดจากจุดที่ปล่อยวัตถุนั้น) ใช้เวลา t วินาที เราจะได้ y = 16t2
ถ้าใช้แกนนอนแทนเวลา t และแกนยืนแทนระยะทางที่วัตถุตกลงมา เขียนกราฟของ y = 16t2 จะได้พาราโบลา
ในการยิงปืนขึ้นสู่อากาศ โดยตั้งปืนให้ทำมุมขนานหนึ่งกับแนวราบ ตามทฤษฎีแล้วกระสุนปืนจะวิ่งไปเป็นแนวเส้นตรง แต่เนื่องด้วยแรงดึงดูดของโลก จะทำให้ระยะทางของกระสุนปืนลดลงมาในแนวดิ่ง ถ้าให้ y' เป็นระยะทางที่กระสุนปืนถูกโลกดูดลงมาในแนวดิ่งในเวลา t วินาที
ดังนั้นจะได้ความสัมพันธ์ระหว่าง t และ y' ตามตาราง t 0 1 2 3 4 5 ... y' 0 16 64 144 256 400 ...
ฉะนั้นเส้นทางที่กระสุนปืนวิ่งไป จึงเป็นเส้นโค้งพาราโบลา และในที่สุดกระสุนปืนก็จะตกลงมากระทบผิวโลก ระยะทางในแนวราบวัดจากจุดที่ยิงปืนไปจนถึงจุดที่ลูกกระสุนกระทบพื้นดิน จะขึ้นอยู่กับขนาดของมุมที่ยิงด้วย (มุมที่ยิงได้ระยะทางในแนวราบไกลที่สุดคือมุม 45 องศา มุมยิงที่เป็นมุมฉากกับแนวราบ กระสุนปืนจะถูกแรงดึงดูดของโลกดูดลงมากระทบศรีษะเราพอดี)
วิถีของจรวดที่ยิงจากจุดหนึ่งไปสู่อีกจุดหนึ่งบนผิวโลกก็เป็นเส้นโค้งพาราโบลา มนุษย์เราสามารถส่งจรวดให้ออกไปเดินทางรอบโลก หรือออกไปสู่สุริยจักรวาลได้ก็โดยให้ความเร็วต้นของจรวดมากพอที่จะพ้นแรงดึงดูดของโลก (ประมาณความเร็ว 18,000 ไมล์ต่อชั่วโมง) และทำให้เส้นทางของจรวดเปลี่ยนจากเส้นโค้งรูปพาราโบลาเป็นรูปวงรี เพราะถ้ายังคงเป็นเส้นแบบรูปพาราโบลาแล้วจรวดจะไม่สามารถกลับมาสู่โลกได้อีกเลย
น้ำพุที่มนุษย์ประดิษฐ์ขึ้นนั้น เราจะสังเกตเห็นได้ว่าสายน้ำพุที่พุ่งขึ้นไปและกลับตกลงมาที่ผิวน้ำอีกนั้น มีลักษณะเป็นเส้นโค้งพาราโบลาขนาดต่างๆ กัน ซึ่งทำให้แลดูสวยงามกว่าการทำให้น้ำพุ่งขึ้นไปและลงมาในแนวดิ่ง
