ฟังก์ชันตรีโกณมิติ (คืออะไร หมายถึง ความหมาย)

ฟังก์ชันตรีโกณมิติ, ฟังก์ชันตรีโกณมิติ หมายถึง, ฟังก์ชันตรีโกณมิติ คือ, ฟังก์ชันตรีโกณมิติ ความหมาย, ฟังก์ชันตรีโกณมิติ คืออะไร

26 พ.ย. 56 05.25 น. | เปิดอ่าน 0 | ความคิดเห็น 0

ฟังก์ชันตรีโกณมิติ (Trigonometric function) คือ ฟังก์ชันของมุม ซึ่งมีความสำคัญในการศึกษารูปสามเหลี่ยมและปรากฏการณ์ในลักษณะเป็นคาบ ฟังก์ชันอาจนิยามด้วยอัตราส่วนของด้าน 2 ด้านของรูปสามเหลี่ยมมุมฉาก หรืออัตราส่วนของพิกัดของจุดบนวงกลมหนึ่งหน่วย หรือนิยามในรูปทั่วไปเช่น อนุกรมอนันต์ หรือสมการเชิงอนุพันธ์ รูปสามเหลี่ยมที่นำมาใช้จะอยู่ในระนาบแบบยุคลิด ดังนั้น ผลรวมของมุมทุกมุมจึงเท่ากับ 180° เสมอ ในปัจจุบัน มีฟังก์ชันตรีโกณมิติอยู่ 6 ฟังก์ชันที่นิยมใช้กันดังตารางข้างล่าง (สี่ฟังก์ชันสุดท้ายนิยามด้วยความสัมพันธ์กับฟังก์ชันอื่น แต่ก็สามารถนิยามด้วยเรขาคณิตได้)
ฟังก์ชันตัวย่อความสัมพันธ์ไซน์ (Sine)sin 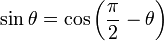$sin heta = cos left(frac{pi}{2} - heta ight) ,$ โคไซน์ (Cosine)cos $cos heta = sin left(frac{pi}{2} - heta ight),$ แทนเจนต์ (Tangent)tan
(หรือ tg) $an heta = frac{1}{cot heta} = frac{sin heta}{cos heta} = cot left(frac{pi}{2} - heta ight) ,$ โคแทนเจนต์ (Cotangent)cot
(หรือ ctg หรือ ctn) $cot heta = frac{1}{ an heta} = frac{cos heta}{sin heta} = an left(frac{pi}{2} - heta ight) ,$ ซีแคนต์ (Secant)sec $sec heta = frac{1}{cos heta} = csc left(frac{pi}{2} - heta ight) ,$ โคซีแคนต์ (Cosecant)csc
(หรือ cosec) $csc heta =frac{1}{sin heta} = sec left(frac{pi}{2} - heta ight) ,$
นิยามจากรูปสามเหลี่ยมมุมฉาก
ในการนิยามฟังก์ชันตรีโกณมิติสำหรับมุม A เราจะกำหนดให้มุมใดมุมหนึ่งในรูปสามเหลี่ยมมุมฉากเป็นมุม A

เรียกชื่อด้านแต่ละด้านของรูปสามเหลี่ยมตามนี้
ด้านตรงข้ามมุมฉาก (hypotenuse) คือด้านที่อยู่ตรงข้ามมุมฉาก หรือเป็นด้านที่ยาวที่สุดของรูปสามเหลี่ยมมุมฉาก ในที่นี้คือ h
ด้านตรงข้าม (opposite side) คือด้านที่อยู่ตรงข้ามมุมที่เราสนใจ ในที่นี้คือ a
ด้านประชิด (adjacent side) คือด้านที่อยู่ติดกับมุมที่เราสนใจและมุมฉาก ในที่นี้คือ b
จะได้

ไซน์ ของมุม คือ อัตราส่วนของความยาวด้านตรงข้าม ต่อความยาวด้านตรงข้ามมุมฉาก ในที่นี้คือ sin(A) = ข้าม/ฉาก = a/h
โคไซน์ ของมุม คือ อัตราส่วนของความยาวด้านประชิด ต่อความยาวด้านตรงข้ามมุมฉาก ในที่นี้คือ cos(A) = ชิด/ฉาก = b/h
แทนเจนต์ ของมุม คือ อัตราส่วนของความยาวด้านตรงข้าม ต่อความยาวด้านประชิด ในที่นี้คือ tan(A) = ข้าม/ชิด = a/b
โคซีแคนต์ csc(A) คือฟังก์ชันผกผันการคูณของ sin(A) นั่นคือ อัตราส่วนของความยาวด้านตรงข้ามมุมฉาก ต่อความยาวด้านตรงข้าม csc(A) = ฉาก/ข้าม = h/a
ซีแคนต์ sec(A) คือฟังก์ชันผกผันการคูณของ cos(A) นั่นคือ อัตราส่วนของความยาวด้านตรงข้ามมุมฉาก ต่อความยาวด้านประชิด sec(A) = ฉาก/ชิด = h/b
โคแทนเจนต์ cot(A) คือฟังก์ชันผกผันการคูณของ tan(A) นั่นคือ อัตราส่วนของความยาวด้านประชิด ต่อความยาวด้านตรงข้าม cot(A) = ชิด/ข้าม = b/a

วิธีจำ
วิธีจำอย่างง่าย ๆ คือจำว่า ข้ามฉาก ชิดฉาก ข้ามชิด ซึ่งหมายความว่า

ข้ามฉาก ... sin = ด้านตรงข้าม/ด้านตรงข้ามมุมฉาก
ชิดฉาก ... cos = ด้านประชิด/ด้านตรงข้ามมุมฉาก
ข้ามชิด ... tan = ด้านตรงข้าม/ด้านประชิด

นิยามด้วยวงกลมหนึ่งหน่วย
ฟังก์ชันตรีโกณมิติทั้ง 6 ฟังก์ชัน สามารถนิยามด้วยวงกลมหนึ่งหน่วย ซึ่งเป็นวงกลมที่มีรัศมียาว 1 หน่วย และมีจุดศูนย์กลางอยู่ที่จุดกำเนิด วงกลมหนึ่งหน่วยช่วยในการคำนวณ และหาค่าฟังก์ชันตรีโกณมิติสำหรับอาร์กิวเมนต์ที่เป็นบวกและลบได้ ไม่ใช่แค่ 0 ถึง π/2 เรเดียนเท่านั้น สมการของวงกลมหนึ่งหน่วยคือ:
$x^2 + y^2 = 1 ,$
เราจะวัดมุมในหน่วยเรเดียน โดยให้มุมเป็นบวกในทิศทวนเข็มนาฬิกา และมุมเป็นลบในทิศตามเข็มนาฬิกา ลากเส้นให้ทำมุม θ กับแกน x ด้านบวก และตัดกับวงกลมหนึ่งหน่วย จะได้ว่าพิกัด x และ y ของจุดตัดนี้จะเท่ากับ cos θ และ sin θ ตามลำดับ เหตุผลเพราะว่ารูปสามเหลี่ยมที่เกิดขึ้นนั้น จะมีความยาวด้านตรงข้ามมุมฉาก ยาวเท่ากับรัศมีวงกลม นั่นคือยาวเท่ากับ 1 หน่วย เราจะได้ sin θ = y/1 และ cos θ = x/1 วงกลมหนึ่งหน่วยช่วยให้เราหากรณีที่สามเหลี่ยมมีความสูงเป็นอนันต์ (เช่น มุม π/2 เรเดียน) โดยการเปลี่ยนความยาวของด้านประกอบมุมฉาก แต่ด้านตรงข้ามมุมฉากยังยาวเท่ากับ 1 หน่วย เท่าเดิม
สำหรับมุมที่มากกว่า 2π หรือต่ำกว่า −2π เราสามารถวัดมุมได้ในวงกลม ด้วยวิธีนี้ ค่าไซน์และโคไซน์จึงเป็นฟังก์ชันเป็นคาบที่มีคาบเท่ากับ 2π:
$sin heta = sinleft( heta + 2pi k ight)$ $cos heta = cosleft( heta + 2pi k ight)$
เมื่อ θ เป็นมุมใดๆ และ k เป็นจำนวนเต็มใดๆ
คาบที่เป็นบวกที่เล็กที่สุดของฟังก์ชันเป็นคาบ เรียกว่า คาบปฐมฐานของฟังก์ชัน คาบปฐมฐานของไซน์, โคไซน์, ซีแคนต์ หรือโคซีแคนต์ จะเท่ากับวงกลมหนึ่งวง นั่นคือเท่ากับ 2π เรเดียน หรือ 360 องศา คาบปฐมฐานของแทนเจนต์ หรือโคแทนเจนต์ จะเท่ากับครึ่งวงกลม นั่นคือเท่ากับ π เรเดียน หรือ 180 องศา
จากข้างบนนี้ ค่าไซน์และโคไซน์ถูกนิยามจากวงกลมหนึ่งหน่วยโดยตรง แต่สี่ฟังก์ชันตรีโกณมิติที่เหลือจะถูกนิยามโดย
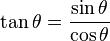
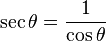
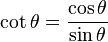
$an heta = frac{sin heta}{cos heta}$ $sec heta = frac{1}{cos heta}$ $csc heta = frac{1}{sin heta}$ $cot heta = frac{cos heta}{sin heta}$

ฟังก์ชันตรีโกณมิติพื้นฐานทั้งหมด สามารถนิยามจากวงกลมหนึ่งหน่วยได้โดยใช้วงกลมหนึ่งหน่วย ที่จุดศูนย์กลางอยู่ที่จุด O ซึ่งคล้ายกับการนิยามเชิงเรขาคณิตที่ใช้กันมาในสมัยก่อน ให้ AB เป็นคอร์ดของวงกลม ซึ่ง θ เป็นครึ่งหนึ่งของมุมที่รองรับคอร์ดนั้น จะได้

sin(θ) คือ ความยาว AC (ครึ่งหนึ่งของคอร์ด) นิยามนี้เริ่มใช้โดยชาวอินเดีย
cos(θ) คือระยะทางตามแนวนอน OC
versin(θ) = 1 − cos(θ) คือ ความยาว CD
tan(θ) คือ ความยาวของส่วน AE ของเส้นสัมผัสที่ลากผ่านจุด A จึงเป็นที่มาของคำว่าแทนเจนต์นั่นเอง (tangent = สัมผัส)
cot(θ) คือ ส่วนของเส้นสัมผัสที่เหลือ คือความยาว AF
sec(θ) = OE และ
csc(θ) = OF เป็นส่วนของเส้นซีแคนต์ (ตัดวงกลมที่จุดสองจุด) ซึ่งสามารถมองว่าเป็นภาพฉายของ OA ตามแนวเส้นสัมผัสที่จุด A ไปยังแกนนอนและแกนตั้ง ตามลำดับ
exsec(θ) = DE = sec(θ) − 1 (ส่วนของซีแคนต์ด้านนอก)

ด้วยวิธีสร้างเหล่านี้ ทำให้เห็นภาพฟังก์ชันซีแคนต์และแทนเจนต์ลู่ออก เมื่อ θ เข้าใกล้ π/2 (90 องศา) และโคซีแคนต์และโคแทนเจนต์ลู่ออก เมื่อ θ เข้าใกล้ศูนย์
นิยามด้วยอนุกรม
โดยการใช้เรขาคณิตและคุณสมบัติของลิมิต เราแสดงได้ว่าอนุพันธ์ของไซน์คือโคไซน์ และอนุพันธ์ของไคโซน์คือค่าลบชองไซน์ เราสามารถใช้อนุกรมเทย์เลอร์สำหรับแสดงเอกลักษณ์ต่อไปนี้สำหรับทุกจำนวนจริง x:
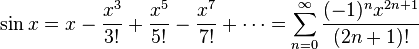
$sin x = x - frac{x^3}{3!} + frac{x^5}{5!} - frac{x^7}{7!} + cdots = sum_{n=0}^infty frac{(-1)^nx^{2n+1}}{(2n+1)!}$ $cos x = 1 - frac{x^2}{2!} + frac{x^4}{4!} - frac{x^6}{6!} + cdots = sum_{n=0}^infty frac{(-1)^nx^{2n}}{(2n)!}$
เอกลักษณ์เหล่านี้มักใช้เป็น นิยาม ของฟังก์ชันไซน์ และโคไซน์ ซึ่งนำไปใช้เป็นจุดเริ่มต้นแบบเข้มของฟังก์ชันตรีโกณมิติ และการประยุกต์ของมัน (เช่น อนุกรมฟูรีเย) เพราะว่ามันมีพื้นฐานอยู่บนระบบจำนวนจริง ไม่ขึ้นกับการตีความทางเรขาคณิตใดๆ การหาอนุพันธ์ได้และความต่อเนื่องของฟังก์ชันก็มาจากนิยามนี้
เอกลักษณ์
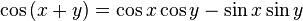
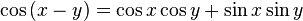
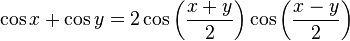
$sin left(x+y ight)=sin x cos y + cos x sin y$ $sin left(x-y ight)=sin x cos y - cos x sin y$ $cos left(x+y ight)=cos x cos y - sin x sin y$ $cos left(x-y ight)=cos x cos y + sin x sin y$ $sin x+sin y=2sin left( frac{x+y}{2} ight) cos left( frac{x-y}{2} ight)$ $sin x-sin y=2cos left( frac{x+y}{2} ight) sin left( frac{x-y}{2} ight)$ $cos x+cos y=2cos left( frac{x+y}{2} ight) cos left( frac{x-y}{2} ight)$ $cos x-cos y=-2sin left( frac{x+y}{2} ight)sin left( frac{x-y}{2} ight)$ $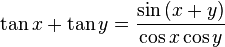an x+ an y=frac{sin left( x+y ight) }{cos xcos y}$ $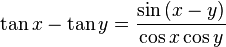an x- an y=frac{sin left( x-y ight) }{cos xcos y}$ $cot x+cot y=frac{sin left( x+y ight) }{sin xsin y}$ $cot x-cot y=frac{-sin left( x-y ight) }{sin xsin y}$
แหล่งที่มา : https://th.wikipedia.org/wiki/ฟังก์ชันตรีโกณมิติ