ลอการิทึม (logarithm) เป็นการดำเนินการทางคณิตศาสตร์ที่เป็นฟังก์ชันผกผันของฟังก์ชันเลขชี้กำลัง ค่าลอการิทึมของจำนวนหนึ่งโดยกำหนดฐานไว้ให้ จะมีค่าเทียบเท่ากับ การเอาฐานมายกกำลังค่าลอการิทึม ซึ่งจะให้คำตอบเป็นจำนวนนั้น ตัวอย่างเช่น
- ลอการิทึมของ 1000 ในฐาน 10 มีค่าเป็น 3 เพราะว่า 10 คูณกัน 3 ตัวแล้วได้ 1000 นั่นคือ 10 × 10 × 10 = 1000
- ลอการิทึมของ 32 ในฐาน 2 มีค่าเป็น 5 เพราะว่า 2 คูณกัน 5 ตัวแล้วได้ 32 นั่นคือ 2 × 2 × 2 × 2 × 2 = 32
ถ้าเขียนด้วยสัญลักษณ์ยกกำลังจะได้ว่า
- 103 = 1000 ดังนั้น log10 1000 = 3
- 25 = 32 ดังนั้น log2 32 = 5
ลอการิทึมของ x ในฐาน b เขียนแทนด้วย logb x หรือถ้าฐานมีค่าใด ๆ เป็นปริยาย จะเขียนเพียงแค่ log x (ไม่จำเป็นต้องใส่วงเล็บรอบ x) ดังนั้นสำหรับจำนวน x ฐาน b และเลขชี้กำลัง y ที่สามารถเป็นไปได้
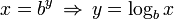
คุณลักษณะหนึ่งที่สำคัญของลอการิทึมคือการลดทอนการคูณไปเป็นการบวกดังนี้
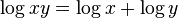
หมายความว่า ลอการิทึมของผลคูณของสองจำนวน จะเท่ากับผลรวมของลอการิทึมของแต่ละจำนวน การใช้ลอการิทึมเพื่อลดทอนการคำนวณที่ซับซ้อนเป็นหนึ่งในแรงผลักดันอย่างมีนัยสำคัญในการพัฒนาที่มีมาแต่เดิม มีการใช้งานลอการิทึมอย่างกว้างขวางทั้งในงานสถิติศาสตร์ เคมี ฟิสิกส์ ดาราศาสตร์ วิทยาการคอมพิวเตอร์ เศรษฐศาสตร์ ดนตรี และวิศวกรรมศาสตร์
สมบัติ
เมื่อ x และ b ถูกกำหนดให้เป็นจำนวนจริงบวก logb x จะให้ผลเป็นจำนวนจริงเพียงหนึ่งเดียว ขนาดหรือค่าสัมบูรณ์ของจำนวนเชิงซ้อนของฐาน b จะต้องไม่เป็น 0 หรือ 1 แต่โดยทั่วไปฐานของลอการิทึมจะเป็น 10, e หรือ 2 มีการนิยามลอการิทึมสำหรับทั้งจำนวนจริงและจำนวนเชิงซ้อนด้วย
สมบัติหลักของลอการิทึมคือการลดทอนการคูณไปเป็นการบวก ซึ่งพัฒนาจากเอกลักษณ์ของการยกกำลัง

เมื่อใส่ลอการิทึมเข้าไปจะได้ว่า

ตัวอย่างเช่น



สมบัติที่เกี่ยวข้องคือการลดรูปยกกำลังไปเป็นการคูณ โดยใช้เอกลักษณ์นี้

ซึ่งเมื่อนำ c ไปยกกำลัง p จะได้ว่า
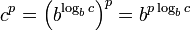
กล่าวโดยนัยได้ว่า การหาค่าจำนวนหนึ่งที่ยกกำลัง p ก่อนอื่นให้หาค่าลอการิทึมฐาน b ของจำนวนนั้นแล้วคูณด้วย p แล้วใส่ผลคูณเป็นเลขชี้กำลังกลับไปยังฐาน b นั่นคือ จำนวนที่ยกกำลัง = b (ผลคูณ) หรือใส่ลอการิทึมเข้าไปจะได้ว่า

ตัวอย่างเช่น

นอกจากการลดรูปการคูณเป็นการบวก และการยกกำลังเป็นการคูณแล้ว ลอการิทึมยังสามารถลดรูปการหารเป็นการลบ และรากเป็นการหาร เช่น
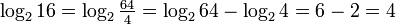
![log_2 sqrt[3]4 = frac{1}{3} log_2 4 = frac{2}{3}](https://upload.wikimedia.org/wikipedia/th/math/f/a/4/fa4720bc4f79762b2b38a168966a74ae.png)
ลอการิทึมทำการดำเนินการทางคณิตศาสตร์อันยืดยาวให้คำนวณง่ายขึ้นโดยการแปลงเป็นการคูณหรือการบวก สำหรับการคำนวณด้วยมือโดยประมาณ สามารถทำได้โดยการเทียบค่าจากตารางลอการิทึม หรือใช้สไลด์รูล สำหรับลอการิทึมสามัญ มีสมบัติหนึ่งที่ปรากฏในการใช้ตารางที่ว่า ลำดับตัวเลขใด ๆ ที่มีค่าเดียวกัน แต่มีค่าประจำหลักต่างกัน จะยังคงให้ แมนทิสซา (mantissa) ค่าเดียวกัน และต่างกันเพียงแค่ แคแรกเทอริสติก (characteristic)
ฟังก์ชันลอการิทึม
ถึงแม้ว่าลอการิทึมเป็นแนวคิดดั้งเดิมของลำดับเลขคณิตของจำนวน ที่สอดคล้องกับลำดับเรขาคณิตของจำนวนอื่น (จำนวนจริงบวก) ดังเช่นที่ให้ความหมายไว้ในสารานุกรมบริตานิกา ค.ศ. 1797 ลอการิทึมยังเป็นผลลัพธ์จากการใช้ฟังก์ชันวิเคราะห์ ฟังก์ชันนั้นสามารถมีความหมายที่ขยายออกไปบนจำนวนเชิงซ้อนได้
ค่าของฟังก์ชัน logb x ขึ้นอยู่กับ b และ x ทั้งสองตัว แต่สำหรับฟังก์ชันลอการิทึมในการใช้งานตามปกติคือฟังก์ชันที่อยู่ในรูปแบบ logb (x) โดยที่ฐาน b เป็นค่าเดียวคงที่ (ซึ่งต้องเป็นจำนวนบวกและไม่เท่ากับ 1) และมี x เป็นอาร์กิวเมนต์เท่านั้น ด้วยเหตุนี้จึงทำให้ฟังก์ชันลอการิทึมของแต่ละค่าบนฐาน b ให้ผลลัพธ์เพียงค่าเดียว ด้วยมุมมองนี้จึงทำให้ฟังก์ชันลอการิทึมฐาน b เป็นฟังก์ชันผกผันของฟังก์ชันเลขชี้กำลัง bx บ่อยครั้งที่คำว่า "ลอการิทึม" หมายถึงฟังก์ชันลอการิทึมโดยตัวมันเองหรือหมายถึงค่าที่ออกมาจากฟังก์ชัน
ลอการิทึมของจำนวนลบหรือจำนวนเชิงซ้อน
มีเพียงจำนวนจริงบวกเท่านั้นที่ให้ผลลัพธ์ของลอการิทึมเป็นจำนวนจริง ฟังก์ชันลอการิทึมสามารถขยายไปได้บนจำนวนเชิงซ้อน ซึ่งครอบคลุมจำนวนลบด้วย และให้ผลเป็นจำนวนเชิงซ้อน แต่ค่าของมันอาจมีมากกว่าหนึ่ง ตัวอย่างเช่น e2πi = e0 = 1 ซึ่งจะทำให้ลอการิทึมฐาน e ของ 1 มีผลลัพธ์เป็นทั้ง 2πi และ 0
เมื่อ z เป็นจำนวนเชิงซ้อนจำนวนหนึ่งซึ่งเขียนได้ในรูปแบบ x + iy โดยที่ x และ y เป็นจำนวนจริง ลอการิทึมของ z สามารถหาได้จากการแปลงเป็นรูปแบบเชิงขั้ว นั่นคือ

โดยที่ r และ θ มาจาก

 คือมุมใดก็ได้ที่ทำให้ x = r cos θ และ y = r sin θ ซึ่งอาจมีมากกว่าหนึ่งค่า
คือมุมใดก็ได้ที่ทำให้ x = r cos θ และ y = r sin θ ซึ่งอาจมีมากกว่าหนึ่งค่า
ถ้าฐานของลอการิทึมถูกเลือกเป็นค่า e นั่นคือใช้ loge หรือ ln อันหมายถึงลอการิทึมธรรมชาติ ดังนั้นลอการิทึมเชิงซ้อนของ z คำนวณได้ดังนี้
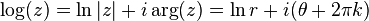
แต่เนื่องจาก arg เป็นฟังก์ชันที่มีผลลัพธ์หลายค่า ดังนั้นจึงมีการนิยามฟังก์ชันใหม่ของลอการิทึมคือ Log (ขึ้นต้นอักษรตัวใหญ่) ซึ่งจะให้ค่าเพียงค่าเดียวดังนี้
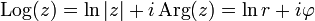
โดยที่ φ จะให้ค่าเพียงค่าเดียวในช่วง (−π, π] ซึ่งมีความหมายเหมือนกับ φ ≡ θ (mod 2π) และ Arg คือฟังก์ชันที่ให้ค่ามุมเพียงค่าเดียวในช่วงดังกล่าว ซึ่งเป็นการนิยามเพิ่มเติมจากฟังก์ชัน arg ฟังก์ชัน Arg นี้เมื่อใช้กับจำนวนจริงจะคืนค่าเป็น 0 ออกมา ซึ่งส่งผลให้พจน์ที่เป็นจำนวนจินตภาพถูกตัดทิ้งไป เหลือแต่ลอการิทึมธรรมชาติของจำนวนจริงเท่านั้น ลอการิทึมธรรมชาติของจำนวนจริงลบ r หาได้จากสูตร

สำหรับลอการิทึมฐานอื่นที่ไม่ใช่ e ลอการิทึมเชิงซ้อน logb (z) สามารถนิยามได้จาก ln (z) / ln (b) ซึ่งแต่ละพจน์ได้นิยามวิธีการคำนวณไว้แล้ว
ในกรณีที่เป็นจำนวนเชิงซ้อน log zp อาจมีค่าไม่เท่ากับ p log z เสมอไป
ทฤษฎีสรุป
จากมุมมองขั้นต้นทางคณิตศาสตร์ เอกลักษณ์นี้

เป็นพื้นฐานของสองเรื่อง ประการแรกคือสมบัติเชิงเลขคณิตทั้งสามอาทิ สมบัติการสลับที่ การเปลี่ยนกลุ่ม การแจกแจง จะยังคงมีอยู่ ประการที่สองคือเอกลักษณ์นี้แสดงให้เห็นสมสัณฐาน (isomorphism) ระหว่างกรุปการคูณของจำนวนจริงบวกกับกรุปการบวกของจำนวนจริงทั้งหมด ฟังก์ชันลอการิทึมเท่านั้นที่เป็นสมสัณฐานอย่างต่อเนื่องระหว่างกรุปดังกล่าว ฐาน
ปกติแล้วฐานของลอการิทึมที่ใช้กันอย่างกว้างขวางได้แก่ 10, e ≈ 2.71828