สนามแม่เหล็ก (คืออะไร หมายถึง ความหมาย)

สนามแม่เหล็ก, สนามแม่เหล็ก หมายถึง, สนามแม่เหล็ก คือ, สนามแม่เหล็ก ความหมาย, สนามแม่เหล็ก คืออะไร

26 พ.ย. 56 05.25 น. | เปิดอ่าน 0 | ความคิดเห็น 1

     สนามแม่เหล็ก นั้นอาจเกิดขึ้นได้จากการเคลื่อนที่ของประจุไฟฟ้า หรือในทางกลศาสตร์ควอนตัมนั้น การสปิน(การหมุนรอบตัวเอง) ของอนุภาคต่างๆ ก็ทำให้เกิดสนามแม่เหล็กเช่นกัน ซึ่งสนามแม่เหล็กที่เกิดจากการ สปิน เป็นที่มาของสนามแม่เหล็กของแม่เหล็กถาวรต่างๆ

      สนามแม่เหล็กคือปริมาณที่บ่งบอกแรงกระทำบนประจุที่กำลังเคลื่อนที่ สนามแม่เหล็กเป็นสนามเวกเตอร์และทิศของสนามแม่เหล็ก ณ ตำแน่งใดๆ คือทิศที่เข็มของเข็มทิศวางตัวอย่างสมดุล

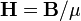       เรามักจะเขียนแทนสนามแม่เหล็กด้วยสัญลักษณ์ $mathbf{B}$ เดิมทีแล้ว สัญลักษณ์ $mathbf{B}$ นั้นถูกเรียกว่าความหนาแน่นฟลักซ์แม่เหล็กหรือความเหนี่ยวนำแม่เหล็ก ในขณะที่ $mathbf{H} = mathbf{B} / mu$ ถูกเรียกว่า สนามแม่เหล็ก (หรือ ความแรงของสนามแม่เหล็ก) และคำเรียกนี้ก็ยังใช้กันติดปากในการแยกปริมาณทั้งสองนี้ เมื่อเราพิจารณาความตอบสนองต่อแม่เหล็กของวัสดุชนิดต่างๆ. แต่ในกรณีทั่วไปแล้ว สองปริมาณนี้ไม่มีความแตกต่างกันมากนัก และเรามักใช้คำแทนปริมาณทั้งสองชนิดว่าสนามแม่เหล็ก

       ในระบบหน่วย SI $mathbf{B}$ และ $mathbf{H}$ นั้นมีหน่วยเป็นเทสลา (T) และ แอมแปร์/เมตร (A/m) หรือในระบบหน่วย cgs หน่วยของทั้งสองคือ เกาส์ (G) และ oersted (Oe)

นิยาม

สนามแม่เหล็กนั้นถูกนิยามขึ้นตามแรงที่มันกระทำ เช่นเดียวกับในกรณีของสนามไฟฟ้า ในระบบหน่วย SI แรงดังกล่าวนี้คือ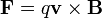

$mathbf{F} = q mathbf{v} imes mathbf{B}$

เมื่อ

F   คือแรงที่เกิดขึ้น วัดในหน่วยนิวตัน
$imes$   เป็นสัญลักษณ์แสดง cross product ของเวกเตอร์
$q$ คือประจุไฟฟ้า วัดในหน่วยคูลอมบ์
$mathbf{v}$ คือความเร็วของประจุไฟฟ้า วัดในหน่วยเมตรต่อวินาที
B   คือความหนาแน่นฟลักซ์แม่เหล็ก วัดในหน่วยเทสลา

กฎด้านบนนี้มีชื่อเรียกว่า กฎแรงของลอเรนซ์
ถ้าประจุที่เคลื่อนที่นั้นเป็นส่วนหนึ่งของกระแสในเส้นลวด กฎด้านบนนี้สามารถเขียนใหม่ได้ในรูป

$frac {dmathbf{F}} {d l} = mathbf{i} imes mathbf{B}$

       หรือพูดอีกอย่างคือ สมการนี้กล่าวว่าแรงที่กระทำต่อหน่วยกระแสไฟฟ้านั้นเท่ากับ cross product ระหว่างเวกเตอร์กระแสและสนามแม่เหล็ก ในสมการนี้ เวกเตอร์กระแส มีขนาดเท่ากับค่าสเกลาร์ (scalar) ของกระแสเช่นทั่วไป () และมีทิศทางชี้ไปในทางที่กระแสไหล

       การเกิดขึ้นของสนามแม่เหล็กนั้น บรรยายได้กระชับและสวยงามที่สุดเมื่อใช้เวกเตอร์แคลคูลัส ดังนี้ (สำหรับกรณีของสุญญากาศ)

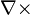$abla imes mathbf{B} = mu_0 mathbf{J} + mu_0 epsilon_0 frac { partial mathbf{E}} {partial t}$ $abla cdot mathbf{B} = 0$

เมื่อ

$abla imes$     คือ โอเปอเรเตอร์ เคิร์ล (curl)
$abla cdot$       คือ โอเปอเรเตอร์ ไดเวอร์เจนซ์ (divergence)
$mu_0$        คือ สภาพให้ซึมได้ของสุญญากาศ
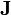$mathbf{J}$          คือ ความหนาแน่นของกระแส
$partial$          คือ อนุพันธ์ย่อย
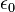$epsilon_0$         คือ สภาพยอมของสุญญากาศ
$mathbf{E}$         คือ สนามไฟฟ้า
$t$           คือ เวลา

        สมการแรกนั้นรู้จักกันในชื่อกฎของแอมแปร์ (หลังการแก้ไขโดยแมกซ์เวลล์) พจน์ที่สองของสมการนี้ (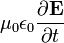 $mu_0 epsilon_0 frac { partial mathbf{E}} {partial t}$ ) จะมีค่าเป็นศูนย์ในกรณีที่ระบบไม่มีการเปลี่ยนแปลง ส่วนสมการที่สองนั้นแสดงให้เห็นว่า magnetic monopole นั้นไม่มีอยู่ ทั้งสองสมการนี้เป็นส่วนหนึ่งของชุดสมการของแมกซ์เวลล์

คุณสมบัติ

        แมกซ์เวลล์มีผลงานชิ้นสำคัญในการรวมปรากฏการณ์ไฟฟ้าและแม่เหล็กเข้าด้วยกัน และสร้างชุดสมการสี่สมการขึ้นเพื่ออธิบายปรากฏการณ์ที่เกี่ยวข้องกับสนามทั้งสองแบบ แต่ด้วยการอธิบายแบบแมกซ์เวลนี้ ยังคงมองปรากฏการณ์ทั้งสองแยกเป็นสนามสองชนิด ซึ่งมุมมองนี้เปลี่ยนไปเมื่อไอน์สไตน์ใช้หลักการของทฤษฎีสัมพัทธภาพพิเศษแสดงให้เห็นว่า ทั้งสองปรากฏการณ์เป็นเพียงด้านสองด้านของสิ่งเดียวกัน (เทนเซอร์ rank 2 อันหนึ่ง) และผู้สังเกตคนหนึ่งอาจจะรับรู้แรงแม่เหล็ก ในขณะที่ผู้สังเกตคนที่สองรับรู้เป็นแรงไฟฟ้าอย่างเดียวก็ได้ ดังนั้นในมุมมองของสัมพัทธภาพพิเศษ สนามแม่เหล็กจึงเป็นเพียงรูปหนึ่งของแรงไฟฟ้าที่เกิดจากประจุที่กำลังเคลื่อนที่อยู่เท่านั้น และสามารถจะคำนวณได้หากเรารู้แรงไฟฟ้าและการเคลื่อนที่ของประจุเทียบกับผู้สังเกต

         เราสามารถใช้การทดลองในจินตนาการแสดงให้เห็นว่าคำกล่าวนี้เป็นจริง โดยพิจารณาเส้นประจุสองเส้นที่ขนานกันและยาวเป็นอนันต์ และอยู่นิ่งเมื่อเทียบกับกันและกัน แต่มีการเคลื่อนที่เทียบกับผู้สังเกตคนแรก. ผู้สังเกตอีกคนหนึ่งซึ่งกำลังเคลื่อนที่ไปกับเส้นประจุทั้งสอง (ที่ความเร็วเท่ากัน) จะรู้สึกได้เฉพาะแรงไฟฟ้าที่ผลักกันระหว่างประจุและความเร่งที่เกิดขึ้นจากแรงนี้ ส่วนผู้สังเกตคนแรกซึ่งอยู่นิ่งมองเห็นเส้นประจุทั้งสอง (และผู้สังเกตคนที่สอง) เคลื่อนที่ผ่านไปด้วยความเร็วค่าหนึ่ง และยังมองเห็นนาฬิกาของผู้สังเกตที่กำลังเคลื่อนที่นั้นเดินช้าลงด้วย (เนื่องจากเวลาหด (time dilation)) และดังนั้นจึงเห็นว่าความเร่งจากแรงผลักกันของเส้นประจุนั้นมีค่าน้อยลงด้วย เทียบกับความเร่งที่ผู้สังเกตคนที่สองรู้สึก การลดลงของความเร่งในทิศทางผลักกันนี้ สามารถมองในแง่กลศาสตร์ดั้งเดิมได้ว่าเป็นแรงดูดนั่นเอง และแรงดูดนี้มีค่ามากขึ้นเมื่อความเร็วสัมพัทธมีค่ามากขึ้น แรงเสมือนนี้ก็คือแรงแม่เหล็กไฟฟ้าในมุมมองเดิมของแมกซ์เวลนั่นเอง

          จากกฎการเหนี่ยวนำของฟาราเดย์ สนามแม่เหล็กที่เปลี่ยนแปลงนั้นสามารถเหนี่ยวนำให้เกิดสนามไฟฟ้า(และกระแสไฟฟ้า) ได้ ปรากฏการณ์นี้เป็นพื้นฐานของเครื่องกำเนิดไฟฟ้าและมอเตอร์ไฟฟ้านั่นเอง

เส้นแรงแม่เหล็ก

        ด้วยนิยามอย่างเป็นทางการแล้ว เส้นแรงแม่เหล็กไม่ได้เป็นปริมาณเวกเตอร์ แต่เป็นเวกเตอร์เสมือน เท่านั้น แม้ว่าภาพต่างๆ มักจะแสดงเส้นแรงแม่เหล็กด้วยลูกศร แต่เราไม่สามารถแปลความหมายลูกศรนั้นเป็นการเคลื่อนที่หรือการไหลของเส้นสนาม

ความสับสนในการเรียกชื่อขั้วแม่เหล็ก

สิ่งสำคัญที่ควรจำคือ ป้ายขั้วเหนือใต้บนเข็มทิศนั้นเรียกสลับกับขั้วเหนือใต้ของแกนโลก

        ถ้าเรามีแม่เหล็กสองอันที่มีป้ายบอกขั้ว ก็ไม่ยากที่จะมองเห็นว่าขั้วเหมือนกันจะผลักกันและขั้วต่างกันดูดกัน แต่การมองแบบนี้ใช้ไม่ได้กับเข็มทิศทั่วไป เพราะสำหรับเข็มทิศแล้ว ด้านที่บอกว่าเหนือชี้ไปทางทิศเหนือไม่ใช่ทิศใต้

        เรานิยมเรียกชื่อขั้วของก้อนแม่เหล็กตามทิศที่มันชี้ไป ดังนั้นเราจึงสามารถเรียกขั้วเหนือของแม่เหล็กได้อีกอย่างหนึ่งว่า ขั้วที่ชี้ไปทางเหนือ

แหล่งที่มา : https://th.wikipedia.org/wiki/สนามแม่เหล็ก